رياضيات الفبايي است كه خداوند جهان را بر مبناي آن خلق كرد.
«گاليله»
(((((برای خواندن مطالب جدید به قسمتهای زیرین پست ثابت بروید)))))
با تشکر : مدیر وبلاگ
ما را از نظرات ارزنده تان بی بهره نکنید .
شما همچنین می توانید به وبلاگ ریاضی من واقع در سایت بلاگفا مراجعه کنید .... mathgroup.blogfa.com
کل مطالب من در آن وبلاگ به صورت لینکهای زیر مرتب می باشد ..
برچسبها:
دانش آموزان باهوش سوم راهنمایی
در آزمون آنلاین ریاضی (سوم راهنمایی) شرکت کنید و خود را محک بزنید.(این آزمون جنبه آزمایشی دارد.)
دانش آموزان عزیز کد ورود به آزمون را از یکی از کدهایی که در ادامه مطلب ذکر شده استفاده کنند.
برچسبها:
ادامه مطلب
سوالات ریاضی سوم ترم دوم (خردادماه1391) از استان های سراسر کشور
از موسسه جویا مجد تهران (ناشر کتاب های ریاضی کامل و.....)که این مجموعه سوالات را در اختیار ما قرار داد متشکریم
|
اذربایجان غربی |
آذربایجان شرقی |
||||
|
چهارمهال وبختیاری |
سیستان وبلوچستان |
||||
بر گرفته از وبلاگ دوست خوبم : ریاضی 20
برچسبها:
نمونه سوالات ترم دوم از سراسر کشور ، ریاضی دوم راهنمایی
با سپاس از موسسه جویا مجد تهران
برچسبها:
99669999996669999996699666699666999966699666699 شماره هاي بالا را انتخاب كنيد سپس Ctrl + F را بزنید سپس شماره 9 را بزنيد و در آخر Ctrl + Enter را بزنيد...
99699999999699999999699666699669966996699666699
99669999999999999996699666699699666699699666699
99666699999999999966666999966699666699699666699
99666666999999996666666699666699666699699666699
99666666669999666666666699666669966996699666699
99666666666996666666666699666666999966669999996
برچسبها:

به استحضار میرساند در پی برگزاری یازدهمین، بیست و دومین و سی و سومین کنفرانس ریاضی ایران در دانشکده علوم ریاضی دانشگاه فردوسی مشهد، این دانشگاه در روزهای 5 الی 8 شهریورماه 1392 میزبانی چهل و چهارمین کنفرانس ریاضی ایران را خواهد داشت.
ثبت نام با ارسال مقاله : اول لغایت 31 اردیبهشت ماه 1392
ثبت نام بدون ارسال مقاله: اول اردیبهشت ماه لغایت 31 خرداد ماه 1392
برای کسب اطلاعات بیشتر به منزلگاه کنفرانس مراجعه فرمایید و یا از طریق رایانامه با دبیرخانه کنفرانس تماس حاصل فرمایید.
منزلگاه: http://imc44.um.ac.ir
رایانامه: imc44@um.ac.ir
برگرفته از سایت : http://www.karamath.ir/
برچسبها:
برای گرفتن یوزر و پسورد نود 32 تا تاریخ 11 فروردین 91 به ادامه مطلب بروید ....
برچسبها:
ادامه مطلب
در ۱۳۲۸ خورشیدی، ریاضیدان هندی، Kaprekar، فرآیندی را ابداع کرد که به عملیات Kaprekar شهرت یافت. در این عملیات، ابتدا عددی ۴ رقمی بایستی انتخاب شود؛ با این شرط که تمام ارقام با یکدیگر یکسان نباشند (مثلا، انتخاب اعدادی مانند ۷۷۷۷ یا ۵۵۵۵ و … نقض شرط است). پس از انتخاب عدد، بایستی ارقام آن عدد را به صورت بزرگترین و کوچکترین عدد مرتب کنیم. مثلا، اگر عدد ۸۴۵۷ را انتخاب کردید، بزرگترین ترتیبش میشود: ۸۷۵۴ و کوچکترین ترتیب نیز میشود: ۴۵۷۸٫ سرانجام، بایستی این دو عدد را از یکدیگر کم کنیم تا عددی جدید به دست آید و این مرحله را تکرار کنیم.
عملیات سادهای است، اما Kaprekar متوجه موضوعی شگفتانگیز شد. اجازه دهید این عملیات را با عدد ۱۳۹۰ امتحان کنیم وقتی که به عدد ۶۱۷۴ رسیدیم و اگر بخواهیم عملیات را ادامه دهیم در هر خط دوباره به عدد ۶۱۷۴ میرسیم. اجازه دهید این بار با عددی دیگر، مثلا با ۶۵۱۷ این عملیات را بررسی کنیم.عملیات اندکی طولانیتر میشود اما باز به همان نتیجه رسیدیم؛ یعنی عدد ۶۱۷۴٫ اگر اعداد دیگر را نیز امتحان کنید همواره به ۶۱۷۴ خواهید رسید؛ این همان اتفاق عجیبی بود که Kaprekar آن را کشف کرد.
این عملیات حداکثر ممکن است ۷ مرحله تکرار شود. بیشتر اعداد ۴ رقمی بدون ارقام تماما یکسان (۲۱۲۴ عدد) سه مرحلهای به ۶۱۷۴ میرسند، پس از آن ۱۹۸۰ عدد ۷ مرحلهای به این نتیجه میرسند.
مشابه این نتیجهی منحصر به فرد تنها در اعداد سه رقمی تکرار شده است. بدین صورت که اگر همین عملیات را برای اعداد سه رقمی تکرار کنیم همواره به ۴۹۵ میرسیم.
------
منبع : http://hellibammath.blogfa.com/
برچسبها:
برای تشکیل و بدست آوردن سه تایی های فیثا غورسی می توان با جایگذاری به جای u و v مقادیری برای a و b و c بدست آورد .
a=2uv
b=u2-v2
c=u2+v2
( به شرط اینکه اولا u و v با هم برابر نبوده
و دوم نسبت به هم اول باشند 1= (u,v)
و سوم اینکه u>v باشد )
به عنوان مثال اگر به u=2 و v=1 بدهیم مقادیر a=4 و b=3 و c=5 را به ما می دهد که با می دانیم با توجه به رابطه فیثاغورس تشکیل یک مثلث قایم الزاویه را می دهد .
32+42=52
16+9=25
برچسبها:
سگی خرگوشی را دنبال می کند که 150 متر جلوتر از خودش است . هر بار که خرگوش چهشی به طول 7 پا ( یک واحد طول) انجام می دهد سگ 9 پا می جهد . سگ در چند خیز به خرگوش می رسد ؟

جواب را بعد از اینکه حل نمودید در ادامه مطلب پسدا نمایید
برچسبها:
ادامه مطلب
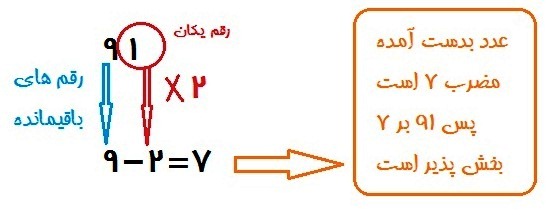
اگر یک عدد دو یا چند رقمی داشتیم برای بخش پذیری بر 7 ،
اول : رقم یکان را جداگانه در 2 ضرب می کنیم .
دوم : رقم های باقی مانده از همان عدد چند رقمی ( منظور به جز رقم یکان) را در نظر گرفته و از مقدار دو برابر رقم یکان ( قسمت قبل)کم می کنیم
سوم : اگر حاصل صفر شود یا عددی مضرب 7 بدست آید آن عدد بر 7 بخش پذیر است .
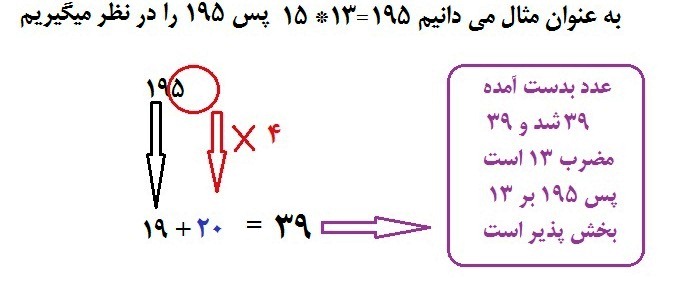
بخش پذیری بر 13 :
اول : رقم یکان را در نظر گرفته و آنرا 4 برابر می کنیم .
دوم : ارقام باقی ماندهاز آن عدد را با حاصل قسمت اول جمع می بندیم
سوم : اگر حاصل عددی مضرب 13 بدست آید آن عدد بر 13بخش پذیر است .
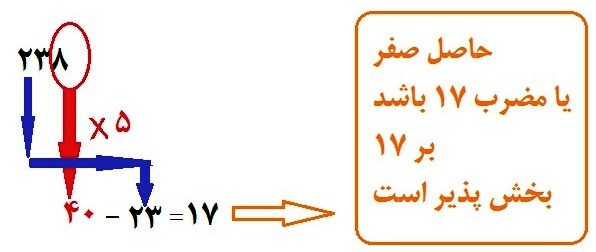
بخش پذیری بر 17:
اول : رقم یکان را در نظر گرفته و آنرا 5 برابر می کنیم .
دوم : سپس ارقام باقی مانده را از حاصل مرحله اول کم می کنیم
سوم : اگر حاصل صفر یا مضرب 17 باشد بر 17 بخش پذیر است
مثال : (می دانیم 238= 17*14 ) 238 را امتحان می کنیم داریم :
برچسبها:
از یکی از دانش آموزان بخواهید تا روز تولد خود را در نظر بگیرید و به شما بگوید که آن عدد روی کدام یک از این کارت ها نوشته شده است .
برچسبها:
ادامه مطلب
معلم ریاضی به دانش آموزان گفت : بعضی از نامساوی ها غیر ممکن است مثلا هیچ عددی از خودش بزرگ تر نیست. ناگهان یک دانش آموز در اومد و گفت : ولی آقا من یه عدد سراغ دارم که از خودش بزرگ تره. معلم با تعجب پرسید چه عددی ؟ دانش آموز گفت آقا ، نیم. معلم گفت چطور؟ دانش آموز گفت: آخه من هر وقت میوه ای را با برادرم قسمت می کنم نصف بزرگ ترش رو برای خودم برمی دارم!
omidimath.loxblog.ir
برچسبها:



